こんにちは。一松です。
前回のSQLの基本に続き、今回は基本として身に付けておきたいアルゴリズムについて書きます。
はじめの一歩として、アルゴリズムを知る上で必要な計算量という考え方と代表的なアルゴリズムの特徴を紹介します。また、これを踏まえてプログラムを書く際の注意点を説明します。
アルゴリズムとは
アルゴリズムとは問題や課題を解決するための処理手順をもれなく表現した考え方のことです。この処理手順の考え方はプログラムの世界だけでなく、みなさんの日常にも使われています。
例えば、「雨が降っていたら傘を持って出かける、雨が降っていなかったら傘を持たずに出かける」、これも短いですがアルゴリズムです。もう少し長いものだと料理のレシピもアルゴリズムの一種といえるでしょう。手順をひとつずつ行うことでおいしい料理が完成しますね。他にもトランプを絵柄ごと数字の小さい順に並び替えることもアルゴリズムを元に考えることができます。
プログラムにおけるアルゴリズムの代表的なものにソート(並び替え)と探索があります。身近なところでは、ショッピングサイトで価格を基準に並び替えを行うときに使われるものがソート、検索エンジンで目的のサイトを探すときに使われるものが探索です。
アルゴリズムと計算量
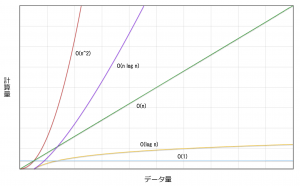
アルゴリズムには結果が出るまでにかかる時間の特徴を表す計算量という考え方があります。入力されるデータ量によって、実行時間がどのような割合で変化するのかを表す指標です。大きくわけると5タイプあります。なお、計算量は一般的に「O記法」という表し方をします。O記法では括弧の中に計算量の増え方の特徴を書きます。例えば、データ数nに対して比例して計算量が増える場合はO(n)と表記します。
・O(1)
データ数nにかかわらず一定なので、nが2倍、3倍、10倍となっても計算量は等しいままです。
・O(n)
比例なので、nが2倍、3倍と増えると、計算量も同様に2倍、3倍となります。
・O(log n)
計算量を求める場合は底を2として考えます。
nが2倍、3倍と増えても、計算量は1、2と増える程度なのでデータ量が多い場合に有用です。
・O(n log n)
先述のO(log n)にnの計算量がかけられたものです。
例えば、nが2倍になると計算量は約2.5倍、nが10倍になると計算量は約20倍、nが100倍になると計算量は約300倍になります。
・O(n^2)
すべての組み合わせを求めるような場合はこのパターンに当てはまります。
n個の要素を用いた総当りの組み合わせを求める場合がこのパターンに当てはまります。
指数関数二次関数なので、nが2倍、3倍と増えると、計算量は4倍、9倍と増えます。
(※本文を訂正しました。2016年8月9日)
図を見てもわかる通り、O(n^2)の計算量では大きなデータを扱うとすぐに現実的な処理時間ではなくなってしまいます。次に紹介する代表的なソートアルゴリズムはO(n^2)のものも紹介していますが、実用的とは言いがたいです。O(log n)のアルゴリズムは膨大なデータ量にも耐えうるので、大量のデータを扱うようなシステムにも導入することができます。
ソートアルゴリズム
ソートとは日本語で言うところの並び替えのことです。小さい順に並べる昇順ソートと、大きい順に並べる降順ソートがあります。
バブルソート
隣り合う要素の大小を比較して整列させます。昇順に並び替える場合は、基準となる要素と隣の要素と比較して、基準の要素のほうが大きければ入れ替え、そうでない場合は入れ替えず、基準となる要素をひとつ隣にずらします。これを繰り返し最終的に正しい順序に並び替えます。隣の要素と比較して要素の最大値(または最小値)が順に決定されていく様子が泡のようなのでバブルソートといいます。要素を並び替えるためにn回比較をし、さらに、その比較をすべての要素で行う必要があるので、計算量はO(n^2)です。
挿入ソート
まず1番目と2番目の要素を比較し、要素の順番が逆ならばいれかえ、正しければそのままにします。次に3番目の要素を正しく並んでいる1番目、2番目の要素と比較し、正しい位置に挿入します。以降の要素もひとつずつ既に並び替えた配列の要素と比較し、正しい順番に並ぶように挿入することを繰り返します。正しく並び替えられた配列に対して直接次の要素を挿入するので、挿入ソートといいます。データの数だけ挿入する回数が増えるので、計算量はO(n^2)です。
マージソート
まず、並び順がばらばらになっている要素を繰り返し2つに切り分け、要素数が1になるまで分解します。分解した配列ごとに大小を比較し並び替えたものを合併していきます。小さく切り分けたソート済の要素を次々に合併して、すべての要素を正しい順番に並び替えます。並び替えの際に合併するのでマージソートといいます。計算量は、はじめに分解する際に2つに切り分けていくのでO(log n)、並び替えの際に要素の数だけ比較をするのでO(n)かかります。よってO(n log n)となります。
探索アルゴリズム
探索とは特定の条件に当てはまるデータを探しだすことです。求める要素と一致する要素が見つかるまで探索をします。
リニアサーチ(線形探索)
一直線に並べたリストを先頭から順に目的の要素かどうか確認していきます。一致する要素が出れば探索終了、一致する要素が出なければ次の要素を確認します。最もシンプルな探索アルゴリズムです。データ量の増加に比例して、比較する要素も増えるので、計算量はO(n)です。
バイナリサーチ(二分探索)
予め対象のデータを昇順に並べておく必要があります。探したいデータと、探したい配列の中央の要素とを比較し、それよりも大きいのか小さいのかによって、次回探す範囲を絞り込みます。例えば、目的の要素が中央の要素より大きければ、大きい方の半分のリストを対象に再度中央の要素を確認し、目的の要素と比較します。このように半分ずつ絞り込んで目的の要素を見つける方法です。中央の要素が探したいデータと一致した時に終了します。1回比較を行うごとに探索の範囲が半分になるので計算量はO(log n)になります。
この他にも代表的なソートアルゴリズムと処理速度の特徴の比較はTECHSCORE BLOGのこちらの記事にまとめられています。
参考:TECHSCOREBLOG「50以下挿入ソート、5万以下マージソート、あとはクイックソート」
なぜ計算量を考える必要があるのか
簡単な擬似プログラムを例に考えてみましょう。
変数wordに代入した単語の文字数(今回はHello!なので6文字)と配列の数を比較し、変数wordに代入された文字数が配列の要素と等しいか大きかった場合に、Hello!と出力されます。
|
1 2 3 4 5 6 7 |
array = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] word = "Hello!" for (i = 0; i < array.length(); i++) { if( array[i] <= word.length()) { print(word) } } |
この処理にかかる時間は、for文の中で都度word.lengthを求める処理をO(n)、その後文字列の数と配列の数字を調べ比較をする処理をO(n)で行うため、n*n=n^2(つまり掛け算)の時間がかかってしまいます。しかし、この時に行うwords.lengthの処理は文字数が一定なので何回ループしても変わることはありません。そこで、for文中での負荷を減らすように変数に代入し、ループの外に出します。
|
1 2 3 4 5 6 7 8 9 |
array = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] word = "Hello" wordLength = word.length() arrayLength = array.length() for (i = 0; i < arrayLemgth; i++) { if(array[i] <= wordLength) { print(word) } } |
あらかじめ、文字列の数をwordLengthとして処理しているため、その都度処理する必要がなくなりました。これによってfor文中の比較は、それぞれの値を読みにいけばよいので、wordの文字数を調べ変数にいれるO(n)、for文中で比較が行われるO(n)を足しあわせて、計算量はn+n=2n(つまり足し算)となり、より小さくすることができます。
最終的な出力は同じであっても、その結果をどのような手順で求めるのかに配慮したプログラムを書くことが重要ですね。(※本文を一部訂正しました。2016年10月17日)
おわりに
アルゴリズムは代表的なソートや探索に使われているものだけではありません。普段私たちが書いているコードも手順を明確に示しているアルゴリズムの一種です。
そこで、アルゴリズムの処理の順番を考え、計算量を意識することで、負荷の少ないプログラムが書けることをご紹介しました。
動くだけのプログラムではなく、よりスマートなコードを書く気づきになれば幸いです。


Comments
> O(n^2)
> すべての組み合わせを求めるような場合はこのパターンに当てはまります。
> 指数関数なので、nが2倍、3倍と増えると、計算量は4倍、9倍と増えます。
n^2は(n に関する)指数関数ではなく、二次関数ではないでしょうか。
また、(それぞれ異なる)要素数 n から k 個を選んだときのすべての
組み合わせ nCk は、n^2 よりも大きい n!/(k!(n-k)!) になりませんか。
ご指摘ありがとうございます。
> すべての組み合わせを求めるような場合はこのパターンに当てはまります。
誤解を生む表現でした。
ここではn個の要素を用いた総当りの組み合わせを求めることがn^2に該当するということを表しています。
> 指数関数なので、nが2倍、3倍と増えると、計算量は4倍、9倍と増えます。
コメントいただいたとおり、指数関数は誤りで、正しくは二次関数です。
本文も合わせて訂正させていただきました。
コメントいただきありがとうございました。
1.array.length() も外に出さない限りO(n)にならないです。
2.計算量はO(n)+O(n)=O(n)です。というか係数を取ったものがOです。もしそういう意図では無く2nと書きたかったのであれば、具体的な係数にしないと意味がありません。(forループ分岐条件の比較も考える)
3.でも結局、計算量をキチンとわからないレベルのプログラマーにお願いする場合はスレッドとか考えると怖すぎるので、重くていいから都度数えてもらったほうがありがたいです。コンパイラも言語によってはかなりお利口さんですしね!
コメントありがとうございます。
>1.array.length() も外に出さない限りO(n)にならないです。
ご指摘いただいたとおりarray.length()をループの外に出すように修正しました。失礼いたしました。
>2.計算量はO(n)+O(n)=O(n)です。というか係数を取ったものがOです。もしそういう意図では無く2nと書きたかったのであれば、具体的な係数にしないと意味がありません。(forループ分岐条件の比較も考える)
今回の記事の対象読者はプログラミング経験が浅く、創意工夫してコードを書くことができないレベルを想定しています。なので、正確性よりも表現として伝わることを優先させていただきました。私が伝えたかったのは計算量が足し算で増えるのか、掛け算で増えるかというレベルの差なので、その意図を補足しました。ご理解の程お願いいたします。
>重くていいから都度数えてもらったほうがありがたいです。コンパイラも言語によってはかなりお利口さんですしね!
コンパイラの最適化の話については、また別の記事で紹介してもいいかもしれませんね。ありがとうございます。